標準正規分布の確率の求め方

(この記事を読むのに必要な時間は約 3 分です。)

なぜこの記事を書くのか？

自分は連続型の確率分布を見た時にこの分布の確率ってどうやって求めるんだっけ？と何度も忘れ、その都度、復習しているので忘れないためにここに書き記しておこうと思ったからです。

まず確率変数とは？

確率変数とは確率的に変動する変数のこと

確率分布とは？

離散型、連続型の2種類があり、確率変数のとる値とその値が実現する確率の関係を表したもの。

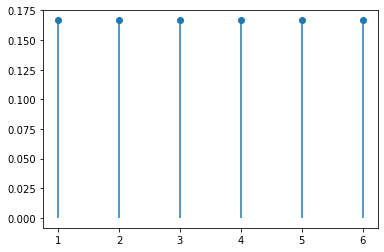
離散型

確率変数が分かれば確率質量関数に代入することで確率を求めることができる

例：二項分布、ポアソン分布

y軸 = P(X)確率質量関数

x軸 = 確率変数(X)

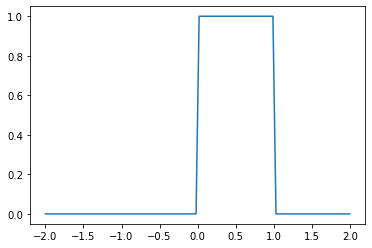
連続型

確率変数が分かれば確率密度関数に代入することで確率を求めることができる

例：正規分布、標準正規分布、t分布、χ²分布、F分布

y軸 = f(x)確率密度関数

x軸 = 確率変数X

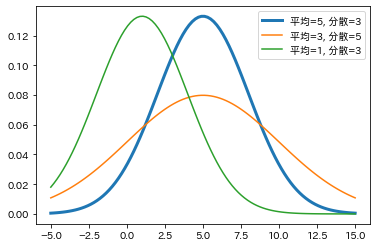
正規分布とは？

X 〜 N(μ, σ²) ※確率変数Xは平均μ分散σ²の正規分布確率分布に従う

平均が変化すると左右に動き、分散が変化すると分布の幅が変化する

y軸 =

x軸 = 確率変数X

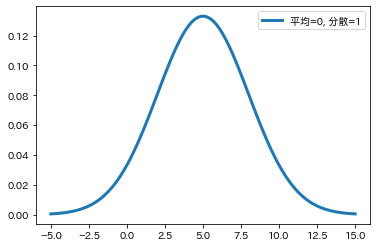
標準正規分布とは？

正規分布を標準化した確率分布

X 〜 N(0, 1) ※確率変数Xは平均0分散1の確率分布に従う

y軸 =

確率密度関数を使って確率を求めてみる

例:標準正規分布において確率変数xが-3以下の確率を求めようと思うと

でも毎回こんな計算をするのは大変・・・

そんな悩みを解決してくれるのが

標準正規分布表！

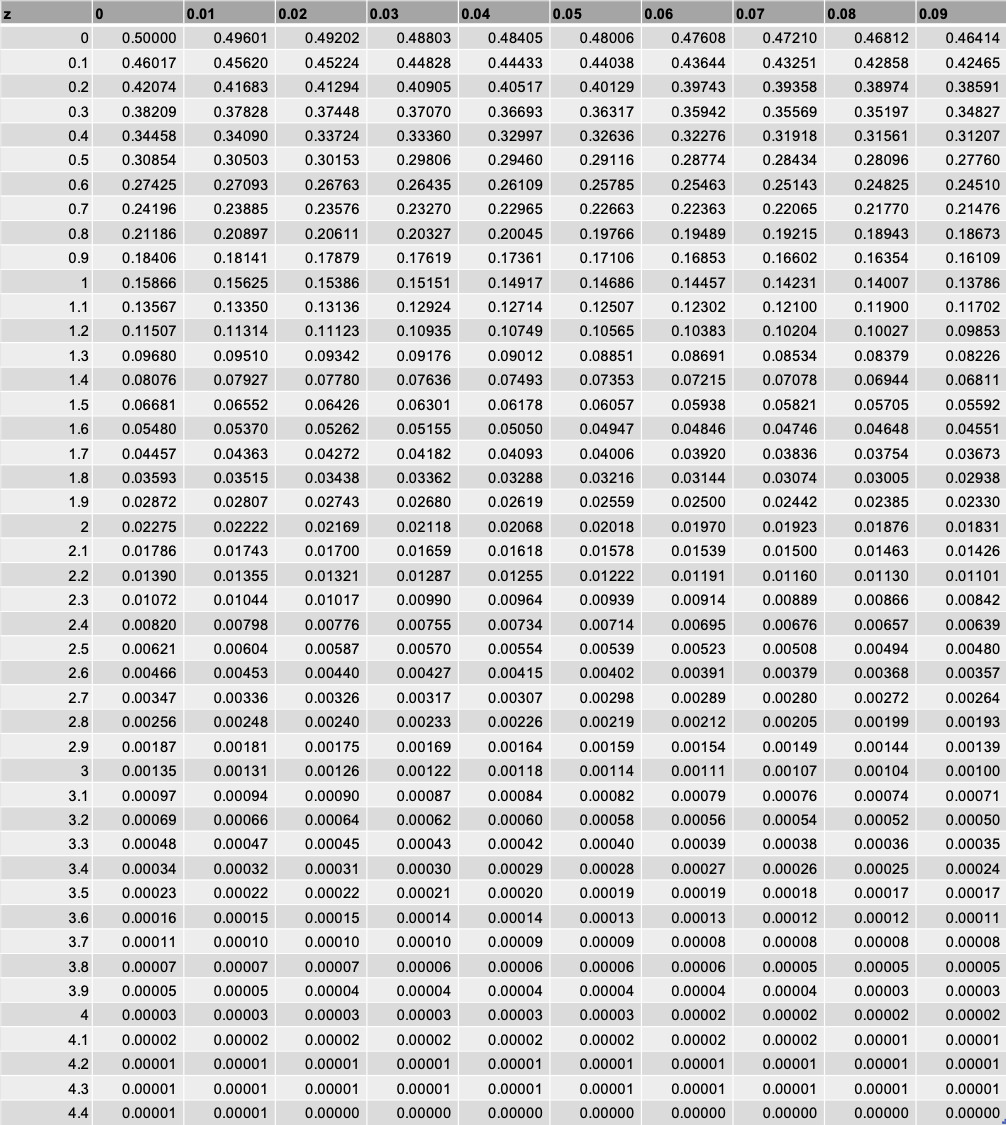
この表に確率を求めたい標準正規分布のZ値(確率変数Xを標準化した値)を当てはめることで確率を求めることができる！